FFTピーク値とエネルギーの件

山岡さんのブログでFFT結果のピーク値使用の注意がありました。

tadaoyamaoka.hatenablog.com

こちらでは主に音声ファイル44.1kHzのファイルフォーマットとラの音440Hzを中心に考察されていましたが、機械系の開発でもFFTを使うことがあり示唆に富んだ内容であるように思います。

具体例として、440Hzのサイン波と435Hzのサイン波のピーク値が

周波数	ピーク値
440Hz	1999.5
435Hz	1527.2

と1.3倍の開きがあり、サンプリング周波数の影響が出ているということを示されています。具体例として機械部品の共振試験を実施した結果に読み替えると、サンプリング周波数を無視して、試験結果のピーク値を読んで共振倍率を求めると痛い目にあうということです。

山岡さんの結果をそのまま使わせていただくと、最悪1.57倍負荷を過小評価してしまう。

これを防ぐためには実際に周波数ドメインの振動を評価する際に、エネルギーの考え方を持ち込む必要があります。まず、スクリプトをお借りして、435Hzと440HzのFFT結果を並べます。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# Sampling Rate
fs = 44100

# Sample Size
size = 4096
t = np.arange(0., size) / fs
frq = np.fft.fftfreq(size, 1./fs)

# 440Hzのサイン波をFFT
f = 440
y = np.sin(2 * np.pi * f * t)
Y = np.fft.fft(y)

# 435Hzのサイン波をFFT
f2 = 435
y2 = np.sin(2 * np.pi * f2 * t)
Y2 = np.fft.fft(y2)

# プロット
plt.plot(frq, abs(Y))
plt.plot(frq, abs(Y2))
plt.axis([300, 500, 0, 2500])
plt.show()

f:id:Chachay:20160828144131p:plain

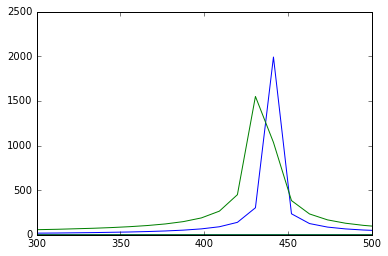
ごらんの通り440Hz(青)と435Hz(緑)で裾の広がり方が違います。 44.1Khz ÷ 周波数の値がより整数に近い440Hzの方がピークがはっきり出ている結果になっています。

これはフーリエ変換を離散化するとつきまとうものですが、 FFTがユニタリ変換なので簡単に(変換前後の)エネルギーの保存を確認できます。

で、それぞれのエネルギーを求めるのは簡単で下記のとおり、

E1 = np.conj(Y)*Y
E2 = np.conj(Y2)*Y2

TTL1 = sum(E1)
TTL2 = sum(E2)

この結果、それぞれの水準でのエネルギーは

周波数	エネルギー値
440Hz	8403716
435Hz	8403443

と、ほぼ一致します。周波数そっくりさんですしね。 (弱冠440Hzの方が大きいのは周波数が高い分、もともと波のエネルギーが高いのです)

当初懸案だったピーク値のような差が大きくなく、評価としてよりロバストだと言えそうですね。

では、ここから、どうやってピーク値を求めるかというと、単純なものから学術的なものまでいろいろあるそうです。入り口としてリンクだけおいておきます。

では！

Volo di notte

お勉強の成果メモや日常のこと

FFTピーク値とエネルギーの件